[Java] Quick Sort(퀵 정렬, 재귀 방식, 왼쪽/중간/오른쪽 피벗)

 

 

---

설명

- 피벗을 기준으로 좌측에 피벗 보다 작은 값, 우측에 피벗보다 큰 값을 위치 시킴

- partition(파티션)을 나눠 행위를 반복한다

- partition을 최소 까지 나눴을 때는 이미 정렬이 완료된 상태이다. 

 

파티션을 나누기 전에 pivot 기준으로 임의 정렬을 하고 partition을 나눠 행위 반복하면 더이상 나눌 수 없을 때 이미 정렬이 완료된다. <-> 반대로 merge sort의 경우 제일 작은 크기 까지 파티션을 먼저 나눈 후 병합을 하면서 정렬 수행한다.

 

*과정

(1) pivot 을 정함

(2) 양쪽 끝에 L, R 포인터를 두고 다음 수행 

    2-1) L < pivot  경우 포인터 증가 L += 1  (pivot 기준 좌변은 항상 작아야 하므로, 큰 값이 나올 때까지 포인터 이동)

    2-2) pivot > R 경우  포인터 감소 R -= 1 (pivot 기준 우변은 항상 커야 하므로, 작은 값이 나올 때 까지 포인터 이동)

    2-3) 탐색 범위 내 일 경우 swap(arr, L, R) 후 재탐색

(3) 포인터가 교차 할 경우, 최종 피벗 위치 기준으로 왼쪽/오른쪽 파티션을 나눠서 1)번부터 반복한다

 

Tip. 개인 기록
- 왼쪽 피벗의 경우 R 포인터를 먼저 움직이고 R을 기준으로 파티션을 나눈다 
- 오른쪽 피벗의 경우 L 포인터를 먼저 움직이고 L을 기준으로 파티션을 나눈다 
- 중앙 피벗의 경우 어느 포인터든 상관없이 교차할 때 (왼쪽, R) , (L, 오른쪽) 파티션을 나눈다
(swap시 L , R 포인터 각각 한칸 씩 이동)

 

영상 참고

https://www.youtube.com/watch?v=h8eyY7dIiN4

 

 

참고. 중앙 피벗 (이미지) 

중앙에 위치한 값을 피벗으로 정하고 양쪽 끝에 포인터 둔다

 

 

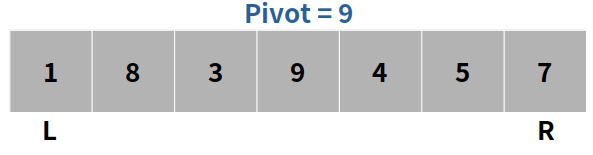
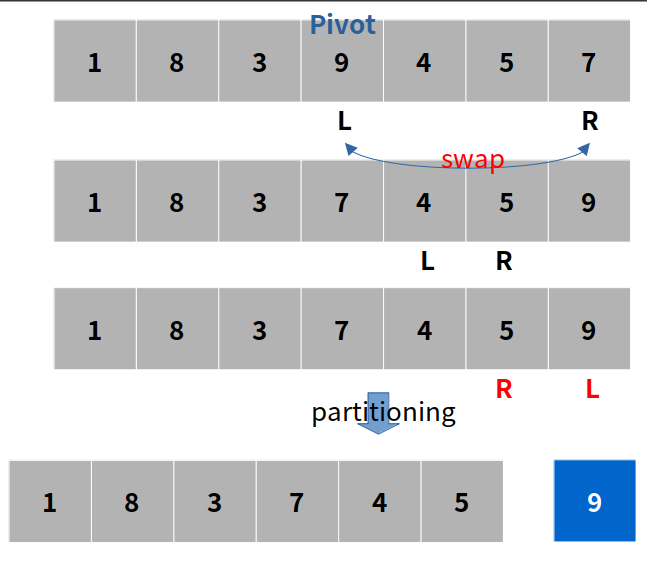
- 파티션 분할 (왼쪽, R) , (L, 오른쪽) 

- (왼쪽, R) 파티션 : quick 정렬 수행

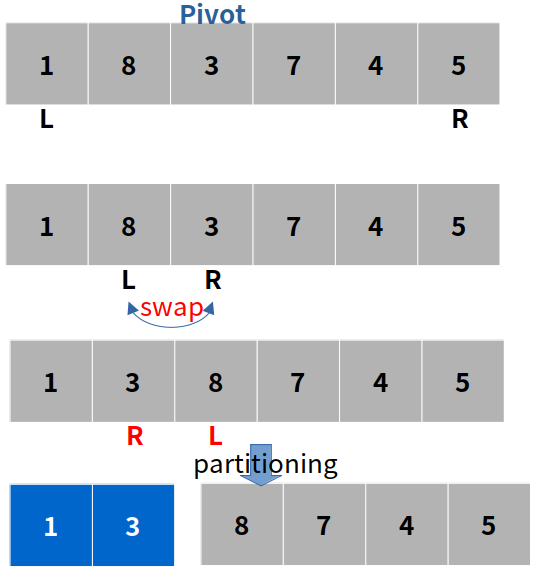
- 파티션 분할 (왼쪽, R) , (L, 오른쪽) 

- (L, 오른쪽) 파티션 : quick 정렬 수행

 

 

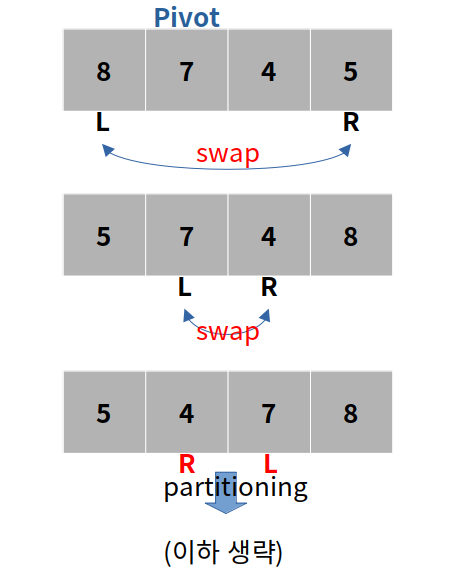
참고. 왼쪽 피벗 (이미지) 

 

 

 

 

참고. 오른쪽 피벗 (이미지) 

 

 

 

코드

1) middle pivot (중앙 피벗)

- L 과 R 이 교차하기 전까지 탐색과 swap 수행

- L > R이 교차했을 때, (시작 인덱스 ~ R), (L ~ 마지막 인덱스) 파티션 분할

private static void quickSort(int[] arr) {
    quickSortByMidPivot(arr, 0, arr.length - 1);
}

private static void swap(int[] arr, int left, int right) {
    int temp = arr[left];
    arr[left] = arr[right];
    arr[right] = temp;
}

private static void quickSortByMidPivot(int[] arr, int leftIdx, int rightIdx) {
    if(leftIdx >= rightIdx) return;

    int mid = (leftIdx + rightIdx) / 2;
    int pivot = arr[mid];
    int L = leftIdx;
    int R = rightIdx;

    while(L <= R) {
        while(arr[L] < pivot) L += 1;
        while(pivot < arr[R]) R -= 1;

        if(L <= R) {
            swap(arr, L, R);
            L += 1;
            R -= 1;
        }
    }

    quickSortByRightPivot(arr, leftIdx, R);
    quickSortByRightPivot(arr, L, rightIdx);
}

public static void main(String[] args) {
    int[] data = new Random().ints(1, 99).distinct().limit(7).toArray();

    System.out.println(Arrays.toString(data));
    quickSort(data);
    System.out.println(Arrays.toString(data));
}

 

2) left pivot(왼쪽 피벗)

- L과 R이 겹치기 전까지 탐색과 swap 수행

- 포인터 R 부터 먼저 움직이고, 파티션을 나눌 때도 R을 기준으로 나눈다

private static void quickSort(int[] arr) {
    quickSortByLeftPivot(arr, 0, arr.length - 1);
}

private static void swap(int[] arr, int left, int right) {
    int temp = arr[left];
    arr[left] = arr[right];
    arr[right] = temp;
}

private static void quickSortByLeftPivot(int[] arr, int leftIdx, int rightIdx) {
    if(leftIdx >= rightIdx) return;

    int pivot = arr[leftIdx];
    int L = leftIdx;
    int R = rightIdx;

    while(L < R) {
        while(pivot < arr[R] && L < R) R -= 1;
        while(arr[L] < pivot && L < R) L += 1;

        if(L >= R) break;

        swap(arr, L, R);
    }

    quickSortByLeftPivot(arr, leftIdx, R - 1);
    quickSortByLeftPivot(arr, R + 1, rightIdx);
}
    
    
public static void main(String[] args) {
    int[] data = new Random().ints(1, 99).distinct().limit(7).toArray();

    System.out.println(Arrays.toString(data));
    quickSort(data);
    System.out.println(Arrays.toString(data));
}

 

3) right pivot (오른쪽 피벗)

- L과 R이 겹치기 전까지 탐색과 swap 수행

- 포인터 L 부터 먼저 움직이고, 파티션을 나눌 때도 L을 기준으로 나눈다

private static void quickSort(int[] arr) {
    quickSortByLeftPivot(arr, 0, arr.length - 1);
}

private static void swap(int[] arr, int left, int right) {
    int temp = arr[left];
    arr[left] = arr[right];
    arr[right] = temp;
}

private static void quickSortByRightPivot(int[] arr, int leftIdx, int rightIdx) {
    if(leftIdx >= rightIdx) return;

    int pivot = arr[rightIdx];
    int L = leftIdx;
    int R = rightIdx;

    while(L < R) {
        while(arr[L] < pivot && L < R) L += 1;
        while(pivot < arr[R] && L < R) R -= 1;

        if(L >= R) break;

        swap(arr, L, R);
    }

    quickSortByRightPivot(arr, leftIdx, L - 1);
    quickSortByRightPivot(arr, L + 1, rightIdx);
}
    
    
public static void main(String[] args) {
    int[] data = new Random().ints(1, 99).distinct().limit(7).toArray();

    System.out.println(Arrays.toString(data));
    quickSort(data);
    System.out.println(Arrays.toString(data));
}

 

 

중앙 피벗 
정렬 전 [3, 27, 16, 97, 57, 35, 20]
정렬 후 [3, 16, 20, 27, 35, 57, 97]

왼쪽 피벗 
정렬 전 [47, 76, 25, 91, 29, 95, 71]
정렬 후 [25, 29, 47, 71, 76, 91, 95]

오른쪽 피벗
정렬 전 [16, 92, 50, 18, 98, 73, 51]
정렬 후 [16, 18, 50, 51, 73, 92, 98]