[프로그래머스] 사칙연산 (Java, DP, lv4)

 

 

---

문제 출처

https://school.programmers.co.kr/learn/courses/30/lessons/1843#

프로그래머스

 

문제 풀이

- 동적 프로그래밍 (dynamic progamming)

- bottom-up 방식 풀이 

 

이 문제에서 주의할 점은 사칙연산에서 +는 결합 법칙이 성립하지만, -는 결합법칙이 성립하지 않는다는 부분이다 

그렇기 때문에 각 구간별 최대값, 최소값을 구한 후 경우의 수를 고려해야 한다 

출처. 나무 위키
한 식에서 연산이 두 번 이상 연속될 때, 앞쪽의 연산을 먼저 계산한 값과 뒤쪽의 연산을 먼저 계산한 결과가 항상 같을 경우 그 연산은 결합법칙을 만족한다고 한다.

실수의 덧셈과 곱셈은 결합법칙을 만족한다. 예를 들어 다음 식은 참이다.
(2 + 3) + 5 = 2 + (3 + 5)

결합법칙이 성립하지 않는 가장 쉬운 예는 실수의 뺄셈일 것이다. 다음 식에서,
(8 - 7) - 3 ≠ 8 - (7 - 3)

출처. https://ko.wikipedia.org/wiki/%EA%B2%B0%ED%95%A9%EB%B2%95%EC%B9%99

 

 

예. a - b 구간이 있을 때 a[0] = 0; a[1] = 1; b[0] = -3; b[1] = 1; (0: 최소값, 1: 최대값) 인 경우 정답은 4가 된다

① a[0] - b[0] = 0 - 1 = -1

② a[0] - b[1] = 0 - (-3) = 3

③ a[1] - b[0] = 1 - (-3) = 4  , a의 최대값과 b의 최소값을 연산했을 때 결과값이 최대가 된다

④ a[1] - b[1] = 1 - 1 = 0

 

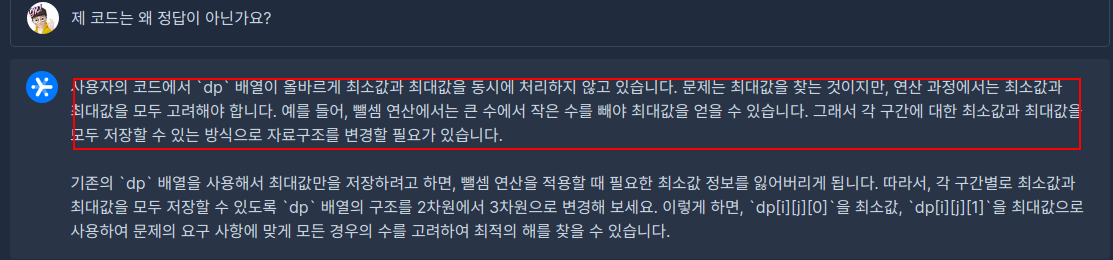
ai 피드백을 받았을 때도 마찬가지로 최소값과 최대값을 고려해야 한다는 것을 언급하였다. (결합법칙에 대한 키워드는 없지만)

 

 

자료구조는 int[][][] dp 3차원 배열을 사용하였다

 

① 구간 길이 1인 경우는 자기 자신으로 최소와 최대값을 초기화 해준다 

int[][][] dp = new int[n + 1][n + 1][2];
for(int i = 1; i <= n; i++) {
    for(int j = 1; j <= n; j++) {
        dp[i][j][0] = Integer.MAX_VALUE;
        dp[i][j][1] = Integer.MIN_VALUE;
    }
}

for(int i = 1; i <= n; i++) {
    dp[i][i][0] = numbers[i];
    dp[i][i][1] = numbers[i];
}

 

 

② len = 2 ~ n 까지 분할 정복으로 경우의 수를 계산하여 값을 채워간다

앞 구간의 최소, 최대와 뒷 구간의 최소, 최대에 대한 4가지 경우의 수를 고려하여 현재 구간의 최대, 최소값을 구한다

for(int len = 2; len <= n; len++) { // 길이 
    for(int i = 1; i <= n - len + 1; i++) { // 시작
        int j = i + len - 1; // 종료
        for(int k = i; k < j; k++) { // 중간 포인터
            // 각 구간의 최소, 최대값에 대한 경우의 수 4가지 고려
            int v1 = calculate(dp[i][k][0], operators[k], dp[k + 1][j][0]);
            int v2 = calculate(dp[i][k][0], operators[k], dp[k + 1][j][1]);
            int v3 = calculate(dp[i][k][1], operators[k], dp[k + 1][j][0]);
            int v4 = calculate(dp[i][k][1], operators[k], dp[k + 1][j][1]);

            int min = Math.min(v1, Math.min(v2, Math.min(v3, v4)));
            int max = Math.max(v1, Math.max(v2, Math.max(v3, v4)));

            dp[i][j][0] = Math.min(dp[i][j][0], min);
            dp[i][j][1] = Math.max(dp[i][j][1], max);
        }
    }
}

 

 

예제 입력1에서 len 3일 때 아래와 같이 분할한다 (길이 1의 경우 둘다 자기 자신이고, 길이2의 경우 둘다 연산 결과)

 

 

③ 최종 결과

예제 입력 1을 처리한 결과는 아래와 같다. 

화살표 방향으로 값을 채워가면 최종적으로 dp[1][n][1], 최대값이 구해진다

 

 

전체 코드 

import java.util.*;

class Solution {
    public int solution(String arr[]) {
        int n = arr.length / 2 + 1;
        int op = arr.length - n;
        int[] numbers = new int[n + 1];
        String[] operators = new String[op + 1];
        
        int idx1 = 1;
        int idx2 = 1;
        for(int i = 0; i < arr.length; i++){
            if(i % 2 == 0) {
                numbers[idx1++] = Integer.parseInt(arr[i]);
            } else {
                operators[idx2++] = arr[i];
            }
        }
 
        // 초기화
        int[][][] dp = new int[n + 1][n + 1][2];
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= n; j++) {
                dp[i][j][0] = Integer.MAX_VALUE;
                dp[i][j][1] = Integer.MIN_VALUE;
            }
        }
        
        // 첫 자리는 자기 자신으로 초기화
        for(int i = 1; i <= n; i++) {
            dp[i][i][0] = numbers[i];
            dp[i][i][1] = numbers[i];
        }
 
        
        for(int len = 2; len <= n; len++) {
            for(int i = 1; i <= n - len + 1; i++) {
                int j = i + len - 1;
                for(int k = i; k < j; k++) {
                    int v1 = calculate(dp[i][k][0], operators[k], dp[k + 1][j][0]);
                    int v2 = calculate(dp[i][k][0], operators[k], dp[k + 1][j][1]);
                    int v3 = calculate(dp[i][k][1], operators[k], dp[k + 1][j][0]);
                    int v4 = calculate(dp[i][k][1], operators[k], dp[k + 1][j][1]);
                    
                    int min = Math.min(v1, Math.min(v2, Math.min(v3, v4)));
                    int max = Math.max(v1, Math.max(v2, Math.max(v3, v4)));
                    
                    dp[i][j][0] = Math.min(dp[i][j][0], min);
                    dp[i][j][1] = Math.max(dp[i][j][1], max);
                }
            }
        }
        
        return dp[1][n][1];
    }
    
    private int calculate(int a, String op, int b) {
        if("+".equals(op)) return a + b;
        
        return a - b;
    }
}