[BOJ 11049] 행렬 곱셈 순서 (Java, DP)

문제 링크
https://www.acmicpc.net/problem/11049
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
문제 풀이
백준 11066 파일 합치기와 비슷한 문제였으나 행렬 곱셉을 어떻게 DP 배열로 처리할 지에 대해 파악하기 힘든 문제였다.
- 상향식(Bottom-Up)으로 풀 경우 시간 복잡도 O(N^2)
- 하향식(Top-Down)으로 풀경우 O(N!) , memorization 기법 활용하여 시간 내에 풀이 가능
- 최대치는 Integer 범위
- 행렬 A (m x k) , B (k x n) 일때 A * B = m x n 행렬이 된다. 이때 연산횟수는 m * k * n 이다.
참고. 행렬의 곱셈
https://mathbang.net/562#gsc.tab=0
행렬의 곱셈, 행렬의 거듭제곱
행렬의 곱셈은 행렬의 실수배에 비하면 훨씬 어려워요. 행렬을 곱할 수 있는 조건이 있어 이 조건을 만족하지 않으면 곱셈을 하지 못하는 경우도 있어요. 게다가 계산방식도 매우 까다롭죠. 도
mathbang.net
여태까지 DP 문제를 풀 경우 행 단위로 순차적으로 채워나가는 형태였다면, 해당 문제의 경우 DP 배열의 경우 사선 방향으로 채워지는 형태를 보임

입력으로 받은 행렬의 r, c값을 하나의 인덱스(객체)라고 생각했을 때 조합을 구하면 아래와 같이 나타난다.

DP[i][j] := i 번째 행렬과 j 번째 행렬의 연산 횟수의 최소값
점화식의 경우 아래와 같다
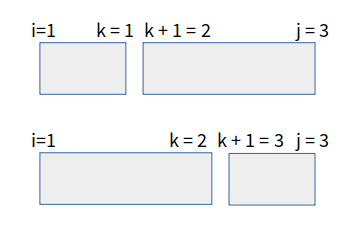
DP[i][j] = Math.min(DP[i][j], DP[i][k] + DP[k + 1][j] + (A[i][0] * A[k + 1][0] * A[j][1])
이때 k 는 i <= k < j
DP[i][j] 에서 i == j인 경우 0 , 그외 초기 최대값 설정
len(길이) = 2인 경우
i = 1 일 때 j = 2 , k = 1 ( 1 <= k < 2 )
DP[1][2] = Math.min(DP[1][2], DP[1][1] + DP[2][2] + (5 * 3 * 2)) = 0 + 0 + 30
i = 2 일 때 j = 3 , k = 2 ( 2 <= k < 3 )
DP[1][2] = Math.min(DP[1][2], DP[2][2] + DP[3][3] + (3 * 2 * 6)) = 0 + 0 + 36
---
len(길이) = 3인 경우
i = 1 일 때 j = 3, k = 1 ( 1 <= k < 3)
DP[1][3] = Math.min(DP[1][3], DP[1][1] + DP[2][3] + (5 * 3 * 6)) = 0 + 36 + 90 = 126
- DP[1][1] = 0
- DP[2][3] 은 2번 행렬과 3번 행렬의 연산 횟수
- 고로 (2번 * 3번) * 1번에 대한 행렬 연산 횟수 구해짐
i = 1 일 때 j = 3, k = 2 ( 1 <= k < 3)
DP[1][3] = Math.min(DP[1][3], DP[1][2] + DP[3][3] + (5 * 2 * 6)) = 30 + 0 + 60 = 90
- DP[1][2] 은 1번 행렬과 2번 행렬의 연산 횟수
- DP[3][3] = 0
- 고로 (1번 * 2번) * 3번에 대한 행렬 연산 횟수 구해짐
제출 코드
(1) Bottom-Up방식
import java.util.*;
import java.io.*;
public class Main {
static StringBuilder sb = new StringBuilder();
static InputProcessor inputProcessor = new InputProcessor();
static int N;
static int[][] MATRIX;
static int[][] DP;
public static void main(String[] args) throws IOException {
input();
preprocess();
bottomUp();
sb.append(DP[1][N]);
output();
}
private static void input() {
N = inputProcessor.nextInt();
MATRIX = new int[N + 1][2];
for(int i = 1; i <= N; i++) {
MATRIX[i][0] = inputProcessor.nextInt();
MATRIX[i][1] = inputProcessor.nextInt();
}
}
private static void preprocess() {
DP = new int[N + 1][N + 1];
for(int i = 1; i < N; i++) {
DP[i][i] = 0;
DP[i][i + 1] = MATRIX[i][0] * MATRIX[i][1] * MATRIX[i + 1][1];
}
}
private static void bottomUp() {
for(int len = 3; len <= N; len++) {
for(int i = 1; i <= N - len + 1; i++) {
int j = i + len - 1;
DP[i][j] = Integer.MAX_VALUE;
for(int k = i; k < j; k++) {
int value = DP[i][k] + DP[k + 1][j] + (MATRIX[i][0] * MATRIX[k][1] * MATRIX[j][1]);
DP[i][j] = Math.min(DP[i][j], value);
}
}
}
}
private static void output() throws IOException {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
bw.write(sb.toString());
bw.flush();
bw.close();
}
private static class InputProcessor {
BufferedReader br;
StringTokenizer st;
public InputProcessor() {
this.br = new BufferedReader(new InputStreamReader(System.in));
}
public String next() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
throw new RuntimeException(e);
}
}
return st.nextToken();
}
public String nextLine() {
String input = "";
try {
input = br.readLine();
} catch (IOException e) {
throw new RuntimeException(e);
}
return input;
}
public int nextInt() {
return Integer.parseInt(next());
}
public long nextLong() {
return Long.parseLong(next());
}
}
}
(2) Top-Down 방식
- DP 배열에서 방문하지 않았다는 의미로 Integer.MAX_VALUE 초기화
import java.util.*;
import java.io.*;
public class Main {
static StringBuilder sb = new StringBuilder();
static InputProcessor inputProcessor = new InputProcessor();
static int N;
static int[][] MATRIX;
static int[][] DP;
public static void main(String[] args) throws IOException {
input();
preprocess();
sb.append(topDown(1, N));
output();
}
private static void input() {
N = inputProcessor.nextInt();
MATRIX = new int[N + 1][2];
for(int i = 1; i <= N; i++) {
MATRIX[i][0] = inputProcessor.nextInt();
MATRIX[i][1] = inputProcessor.nextInt();
}
}
private static void preprocess() {
DP = new int[N + 1][N + 1];
for(int i = 1; i < N; i++) {
Arrays.fill(DP[i], 1, N + 1, Integer.MAX_VALUE);
DP[i][i] = 0;
DP[i][i + 1] = MATRIX[i][0] * MATRIX[i][1] * MATRIX[i + 1][1];
}
}
private static int topDown(int a, int b) {
if(a == b) return DP[a][b];
if(DP[a][b] != Integer.MAX_VALUE) return DP[a][b];
for(int k = a; k < b; k++) {
int value = topDown(a, k) + topDown(k + 1, b) + (MATRIX[a][0] * MATRIX[k][1] * MATRIX[b][1]);
DP[a][b] = Math.min(DP[a][b], value);
}
return DP[a][b];
}
private static void output() throws IOException {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
bw.write(sb.toString());
bw.flush();
bw.close();
}
private static class InputProcessor {
BufferedReader br;
StringTokenizer st;
public InputProcessor() {
this.br = new BufferedReader(new InputStreamReader(System.in));
}
public String next() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
throw new RuntimeException(e);
}
}
return st.nextToken();
}
public String nextLine() {
String input = "";
try {
input = br.readLine();
} catch (IOException e) {
throw new RuntimeException(e);
}
return input;
}
public int nextInt() {
return Integer.parseInt(next());
}
public long nextLong() {
return Long.parseLong(next());
}
}
}