패스트캠퍼스 JavaScript 코딩테스트 강의 4주차

온라인 코드 테스트 사이트
https://www.jdoodle.com/execute-nodejs-online/
Ch 10. 최단 거리
다익스트라 알고리즘(Dijkstra Algorithm)
- 시작 노드를 기준으로 다른 모든 노드로 가는 최단 경로를 계산
- 간선의 가중치가 양수(>= 0)인 경우에 최단 거리를 구할 수 있음
- 다익스트라 알고리즘은 그리디(탐욕) 알고리즘으로 분류됨
=> 매 상황에서 가장 비용이 작은 노드를 선택해 알고리즘 과정을 반복함
- 시간 복잡도 : O(ElogV)
다익스트라 알고리즘의 기본적인 구조/절차는 아래와 같다
* 알고리즘 동작과정
1. 출발 노드 설정
2. 최단 거리 테이블 초기화 (이때, 출발 노드는 0, 그 외는 INF)
3. 방문하지 않은 노드 중에서 "최단 거리가 가장 짧은 노드를 선택"
- 우선 순위 큐, 최소 힙을 사용하여 가중치 작은거 선택
- 이때 가치가 없는 정보의 경우 조건문을 통해 필터링함
예) a -> c 로 5에 가는 정보 찾았을 때, 후에 a -> c 로 10에 가는 정보는 가치가 없기 때문에 조회할 필요 없어 필터링
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 최단 거리 테이블을 직접 갱신하지 않고, 우선 순위 큐에 삽입하는 방식을 사용할 수 도 있다.
5. 위 과정에서 3,4번을 반복한다.
let INF = 1e9; // 10억
let n = 7;
let start = 1; // 시작 노드 번호
// 각 노드에 연결되어 있는 노드 정보를 담는 인접 리스트
let graph = [
[], // 연산 편의 위해
[[2, 3], [3, 1], [4, 2]], // 1번 노드의 간선들
[[1, 3], [3, 1], [5, 1]], // 2번 노드의 간선들
[[1, 1], [2, 1], [4, 3], [6, 5]],
[[2, 1], [6, 2]],
[[3, 5], [5, 2]],
[[3,5], [5,2]],
[[4,1]] // 7번 노드의 간선들
]
// 최단 거리 테이블을 모두 무한으로 초기화
let distance = new Array(n + 1).fill(INF);
function dijkstra() {
// 출발 노드 설정
let pq = new PriorityQueue((a, b) => b[0] - a[0]); // 최소힙(Min Heap)
pq.enq([start, 0]); // (노드, 비용)
// 출발 노드 비용 0으로 초기화
distance[start] = 0;
while(pq.size() != 0) {
let [now, dist] = pq.deq();
// 현재 노드가 이미 처리된 적 있고, 현재 가중치가 더 큰 경우 무시
if(distance[now] < dist) continue;
// 현재 노드와 연결된 다른 인접 노드들을 확인
for(let [nextNode, nextCost] of graph[now]) {
let cost = dist + nextCost; // 다음 노드로 가는 비용
// 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if(cost < distance[nextNode]) {
distance[nextNode] = cost;
pq.enq([nextNode, cost]);
}
}
}
}
// 다익스트라 알고리즘 수행
dijkstra();
// 모든 노드를 가기 위한 최단 거리 출력
for(let i = 1; i <= n; i++) {
if(distance[i] === INF) console.log('INFINITY');
else console.log(distance[i]);
}
우선 순위 큐 모듈 라이브러리를 클래스화하여 사용(priorityqueuejs모듈)
class PriorityQueue {
constructor(comparator) {
this._items = [];
this._comparator = comparator;
}
enq(item) {
this._items.push(item);
let current = this.size() - 1;
while(current > 0) {
let parent = Math.floor((current - 1) / 2);
if(this.compareTo(parent, current) <= 0) break;
this.swap(parent, current);
current = parent;
}
}
deq() {
const first = this.peek();
let last = this._items.pop();
if(this.isEmpty()) return first;
this._items[0] = last;
let index = 0;
let size = this.size();
//최소 힙이고, 자식이 둘 다 있을 때 left, right 중 가장 작은 값과 heapify 수행
while(index < size) {
let target = index;
let left = (2 * index) + 1;
let right = left + 1;
if(left < size && this.compareTo(target, left) >= 0) {
target = left;
}
if(right < size && this.compareTo(target, right) >= 0) {
target = right;
}
if(index === target) break;
this.swap(index, target);
index = target;
}
return first;
}
isEmpty() {
return this.size() === 0;
}
peek() {
if(this.isEmpty()) throw new Error('PriorityQueue is Empty');
return this._items[0];
}
size() {
return this._items.length;
}
swap(a, b) {
const temp = this._items[a];
this._items[a] = this._items[b];
this._items[b] = temp;
}
compareTo(a, b) {
return this._comparator(this._items[a], this._items[b]);
}
forEach(callBack) {
return this._items.forEach(callBack);
}
}
// 테스트
const pq = new PriorityQueue((a, b) => a - b); // 오름차순,minHeap, 최소힙
pq.enq(15);
pq.enq(10);
pq.enq(8);
pq.enq(5);
pq.enq(4);
pq.enq(20);
pq.forEach(item => console.log(item)); // 4 5 10 15 8 20
pq.deq(); // 4
pq.forEach(item => console.log(item)); // 5 8 10 15 20
참고
플로이드 워셜 알고리즘(Floyd-Warshall Algorithm)
- 모든 노드에서 다른 모든 노드까지의 최단 거리를 모두 계산
- 다익스트라 알고리즘과 마찬가지로 단계별 거쳐 가는 노드(k)를 기준으로 알고리즘을 수행함
- 2차원 테이블에 최단 거리 정보 저장함
- 간선의 가중치가 음수인 경우에도 최단 거리를 구할 수 있음 (단, 음수 사이클은 처리 못함)
- 상대적으로 알고리즘 난이도가 낮다
- 시간 복잡도 : O(N^3)
점화식
D[A][B] = min(D[A][B], D[A][K] + D[K][B]);
A -> B로 가는 비용(가중치)과, K를 거쳐 A -> K -> B 로 가는 비용(가중치) 중 무엇이 더 짧은지 검사함
const INF = 1e9;
const n = 4; // 노드의 개수
// graph[i][j] 는 i -> j로 가기 위한 초기 간선 비용
// 예시는 위키 백과 참고
const graph = [
[INF, INF, INF, INF, INF],
[INF, 0, INF, -2, INF],
[INF, 4, 0, 3, INF],
[INF, INF, INF, 0, 2],
[INF, INF, -1, INF, 0]
]
// 점화식에 따라 플로이드 워셜 알고리즘 수행
for(let k = 1; k <= n; k++) {
for(let a = 1; a <= n; a++) {
for(let b = 1; b <= n; b++) {
graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
// 결과 출력
for(let a = 1; a <= n; a++) {
let line = '';
for(let b = 1; b <= n; b++) {
// 도달할 수 없는 경우, 무한(INFINITY)로 출력
if(graph[a][b] === INF) line += 'INF ';
else line += `${graph[a][b]} `;
}
console.log(line);
}
참고
플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm)이란?
벨만 포드 알고리즘
- 매번 모든 간선을 전부 확인 => 기본적으로 다익스트라 알고리즘의 최적의 해를 항상 포함
- 음의 간선이 포함된 상황에서도 사용 가능 (음수 순환, 음의 사이클 탐지 가능)
- 시간 복잡도 : O(VE)
- 상대적으로 다익스트라 알고리즘 보다 느리다.
절차
1. 출발 노드 설정
2. 최단 거리 테이블 초기화
3. 다음 과정을 N - 1번 반복한다
3-1) 전체 간선 E개를 한번씩 확인
3-2) 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다
만약 음수 순환 발생을 체크하고 싶으면 3번의 과정을 한번 더 수행한다.
이때 최단 거리 테이블이 갱신된다면 "음수 순환이 존재"하는 것이다.
참고
동빈나 유튜브 채널 - 코딩 테스트를 위한 벨만 포드 알고리즘 7분 핵심 요약
1) 음수 간선 있는 경우

2) 음수 순환이 발생한 경우
(i === n - 1) 이 될 때까지 최단 거리 갱신이 발생하여 음수 순환을 검출 확인 가능하다
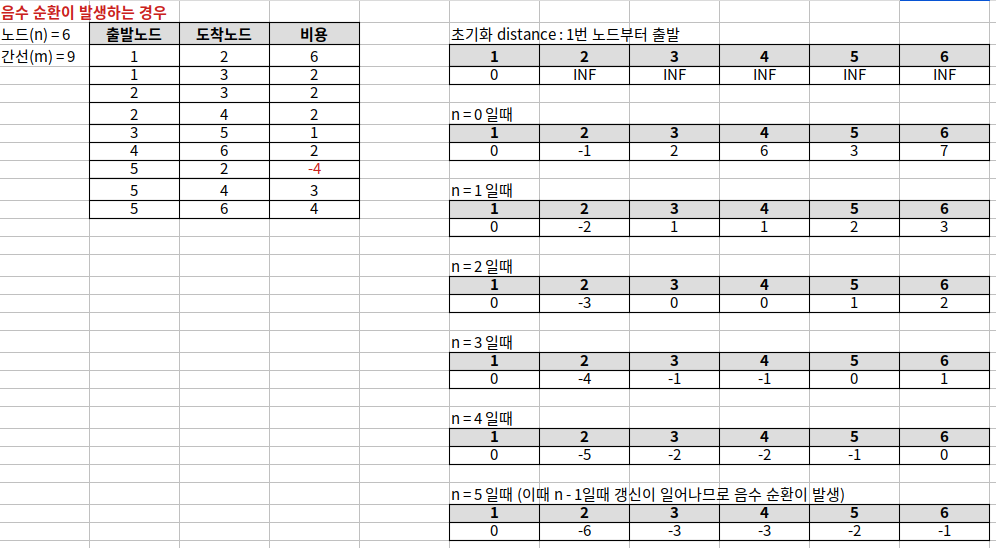
관련 문제) 백준 11657 타임머신
- 벨만 포드 알고리즘 기본 구조에 맞춰 요구사항을 출력해주면 되는 문제
// SUCCESS
const file = require('fs').readFileSync('/dev/stdin').toString().split('\n');
const [n, m] = file[0].split(' ').map(Number); // n : 도시의 개수(노드), m : 버스 노선의 개수(간선)
const info = file.slice(1, m + 1).map(line => line.split(' ').map(Number));
const INF = 1e9;
const distance = new Array(n + 1).fill(INF);
function bellmanFord(start) {
distance[start] = 0;
for(let i = 0; i < n; i++) {
for(let j = 0; j < m; j++) {
const [currentNode, nextNode, cost] = info[j];
if(distance[currentNode] !== INF && distance[nextNode] > distance[currentNode] + cost) {
distance[nextNode] = distance[currentNode] + cost;
if(i === n - 1) return true;
}
}
}
return false;
}
if(bellmanFord(1)) { // 음수 순환 확인되는 경우
console.log(-1);
} else { // 1번 노드 다음부터 출력
for(let i = 2; i <= n; i++) console.log(distance[i] === INF ? -1 : distance[i]);
}
문제 1-1) 플로이드(골드4)
- 플로이드 워셜 알고리즘 기본 문제
- 모든 노드에서 다른 모든 노드까지의 최단 거리를 모두 계산
- 시간 복잡도 : O(N^3)
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const INF = 1e9;
const n = Number(input[0]);
const m = Number(input[1]);
const graph = Array.from({length : n + 1}, () => new Array(n + 1).fill(INF));
const lines = input.slice(2, m + 2).map(line => line.split(' ').map(Number));
for(let i = 1; i <= n; i++) graph[i][i] = 0;
for(let [a, b, c] of lines) {
graph[a][b] = Math.min(graph[a][b], c);
}
for(let k = 1; k <= n; k++) {
for(let a = 1; a <= n; a++) {
for(let b = 1; b <= n; b++) {
graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
for(let a = 1; a <= n; a++) {
let result = '';
for(let b = 1; b <= n; b++) {
if(graph[a][b] === INF) result += `0 `;
else result += `${graph[a][b]} `;
}
console.log(result);
}
문제 1-2) 친구(실버2)
- 플로이드 워셜 알고리즘 응용 문제
- Y = 1 , 자기자신 = 0, 그외 INF로 초기화 후 플로이드 워셜 돌림. 'row별 거리가 2 이하인 친구 수' 중에 최대값 구하면 됨
친구의 수 2이하인 그래프를 어떻게 형상할 지 생각나지 않아 어려웠음
- row 별로 갈 수 있는 연결 노드(1 -> 1, 1 -> 2, ..)를 나타내기 때문에 최단 거리 2이하인 경우만 조건 만족
- 직접 가거나(A -> B), 다른 노드를 거치거나(A -> X -> B) 했을 때 비용(가중치Y는 1로 생각)이 플로이드 워셜로 구함
5
NYNNN
YNYNN
NYNYN
NNYNY
NNNYN
초기화
[ INF, INF, INF, INF, INF, INF ],
[ INF, 0, 1, INF, INF, INF ],
[ INF, 1, 0, 1, INF, INF ],
[ INF, INF, 1, 0, 1, INF ],
[ INF, INF, INF, 1, 0, 1 ],
[ INF, INF, INF, INF, 1, 0 ]
플로이드 워셜
[ INF, INF, INF, INF, INF, INF ],
[ INF, 0, 1, 2, 3, 4 ], -- 1번 : 2 // (1,5)를 가려면 4번을 거쳐야 함
[ INF, 1, 0, 1, 2, 3 ], -- 2번 : 3
[ INF, 2, 1, 0, 1, 2 ], -- 3번 : 4* // 2이하인 최대 친구 수
[ INF, 3, 2, 1, 0, 1 ], -- 4번 : 3
[ INF, 4, 3, 2, 1, 0 ] -- 5번 : 3

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const INF = 1e9;
const n = Number(input[0]); // 노드의 개수
// i -> j로 가기 위한 초기 비용(간선비용)
const graph = [new Array(n + 1).fill(INF)];
for(let i = 1; i <= n ; i++) {
graph.push(new Array(n + 1).fill(INF));
const line = input[i].split('');
for(let j = 0; j < n; j++) {
if(line[j] === 'Y') graph[i][j + 1] = 1;
}
}
for(let i = 1; i <= n; i++) graph[i][i] = 0;
// 점화식에 따라 플로이드 워셜 알고리즘을 수행
for(k = 1; k <= n; k++) {
for(a = 1; a <= n; a++) {
for(b = 1; b <= n; b++) {
graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
// A에서 B로 가는 최단 경로 확인
const distance = new Array(n + 1).fill(0);
for(let i = 1; i <= n; i++) {
for(let j = 1; j <= n; j++) {
if(i !== j && graph[i][j] <= 2) distance[i] += 1;
}
}
console.log(distance.reduce((a, b) => Math.max(a,b)));
문제 1-3) 최단경로(골드4)
- 다익스트라 알고리즘 절차대로 푸는 기본 문제
- 우선 순위 큐 클래스 정의로 인해 시간 소비 많이 함
- 강의에서는 npm으로 모듈 설치후 사용하는 방법을 설명하지만, 백준에 문제 제출 하기 위해서는 class로 정의해서 사용하는 방법밖에 생각이 안났음 (deq() 정의에서 실수 많이함)
- 인강에서 추천해준 모듈을 그대로 class 화하여 문제 풀이함 (default comparator는 생략)
- 시간복잡도 : O(ElogV)
function dijkstra(start) {
let pq = new PriorityQueue((a, b) => a[1] - b[1]);
pq.enq([start, 0]); // 시작노드, 비용
distance[start] = 0;
while(pq.size() > 0) {
let [now, cost] = pq.deq();
if(distance[now] < cost) continue;
for(let [nextNode, nextDistance] of graph[now]) {
let newCost = distance[now] + nextDistance;
if(distance[nextNode] > newCost) {
distance[nextNode] = newCost;
pq.enq([nextNode, newCost]);
}
}
}
}
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [v, e] = input[0].split(' ').map(Number);
const k = Number(input[1]);
const graph = [];
for(let i = 0; i <= v; i++) graph.push([]);
const lines = input.slice(2, e + 2).map(line => line.split(' ').map(Number));
for(let [f, t, c] of lines) {
graph[f].push([t, c]);
}
const INF = 1e9;
const distance = new Array(v + 1).fill(INF);
dijkstra(k);
console.log(distance.map(value => (value === INF ? "INF" : value)).slice(1).join("\n"));
문제 3-1) 특정한 최단 경로(골드4)
u, v를 꼭 거쳐서 1 -> N으로 가야 하기 때문에 아래 두가지 경우에 중 최단 거리를 고른다 ( 없는 경우 -1 )
1 -> u -> v -> N
1 -> v -> u -> N
X -> Y 로 갈때 K를 거쳐 가야 한다면
최단 경로 = (X -> K) + (K -> Y)
function dijkstra(from, to) {
const pq = new PriorityQueue((a, b) => a[1] - b[1]);
pq.enq([from, 0]);
const distance = new Array(n + 1).fill(INF);
distance[from] = 0;
while(pq.size() > 0) {
const [now, dist] = pq.deq();
if(distance[now] < dist) continue;
for(let [nextNode, nextCost] of graph[now]) {
let cost = distance[now] + nextCost;
if(distance[nextNode] > cost) {
distance[nextNode] = cost;
pq.enq([nextNode, cost]);
}
}
}
return distance[to];
}
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const INF = 1e9;
const [n, e] = input[0].split(' ').map(Number);
const lines = input.slice(1, e + 1).map(line => line.split(' ').map(Number));
const graph = [];
for(let i = 0; i <= n; i++) graph.push([]);
for(let [f, t, c] of lines) {
graph[f].push([t, c]);
graph[t].push([f, c]);
}
const [u, v] = input[e + 1].split(' ').map(Number);
// 1 -> u -> v -> N
let result1 = 0;
result1 += dijkstra(1, u);
result1 += dijkstra(u, v);
result1 += dijkstra(v, n);
// 1 -> v -> u -> N
let result2 = 0;
result2 += dijkstra(1, v);
result2 += dijkstra(v, u);
result2 += dijkstra(u, n);
let answer = -1;
if(result1 < INF && result2 < INF) answer = Math.min(result1, result2);
console.log(answer);
심화문제
문제 2-1) 도로포장(골드1)
문제 2-2) 개코전쟁(플래티넘5)
문제 3-2) 거의 최단 경로(플래티넘5)
Ch 11. 투 포인터
문제 1-1) 블로그(실버3)
- 슬라이딩 윈도우 기법 사용하여 문제 풀이
비교
| 참고 블로그 | 투 포인터 | 슬라이딩 윈도우 |
| 구간의 넓이가 | 조건에 따라 유동적으로 변함 | 항상 고정되어 있음 |
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n, x] = input[0].split(' ').map(Number);
const arr = input[1].split(' ').map(Number);
// 초기 sum값 구함
let sum = 0;
for(let i = 0; i < n; i++) {
if(i < x) sum += arr[i];
}
// 슬라이딩 윈도우 기법
let maxSum = sum;
let left = 0;
let right = x - 1;
let count = 1; // *여기 미스
while(true) {
left += 1;
right += 1;
if(right >= n) break;
sum = sum + arr[right] - arr[left - 1];
if(sum > maxSum) {
maxSum = sum;
count = 1;
} else if(sum === maxSum) {
count += 1;
}
}
if(maxSum === 0) {
console.log("SAD");
} else {
console.log(maxSum);
console.log(count);
}
문제 1-2) 가장 긴 짝수 연속한 부분 수열(large) (골드5)
- 최대 k 개(1 또는 k개)만큼의 홀수를 제거한 '짝수로 이루어진 연속한 부분 수열' 중에서 가장 긴 길이 찾는 문제
강의 답안
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n, k] = input[0].split(' ').map(Number); // n : 수열의 길이, k : 최대 횟수
const arr = input[1].split(' ').map(Number); // 수열
let result = 0;
let eraseCount = 0;
for(let start = 0, end = 0; start < n; start++) {
while(end < n) {
if(arr[end] % 2 === 0) { // 짝수인 경우
end += 1;
} else {
if(eraseCount === k) break;
eraseCount += 1;
end += 1;
}
}
result = Math.max(result, end - start - eraseCount); // 범위의 길이 계산
// start를 한 칸 오른쪽으로 이동할 때, 가능하다면 지울 수 있는 개수 증가
if(arr[start] % 2 === 1) eraseCount -= 1;
}
console.log(result);
입력 예시
8 2
1 2 3 4 5 6 7 8
정답
3
0 4 2 2 -- start, end, eraseCount, result
1 6 2 3
2 6 2 3
3 8 2 3
4 8 2 3
5 8 1 3 -- 최대 k개까지 삭제 가능하니 1개도 가능
6 8 1 3
7 8 0 3
문제 1-3) 배열 합치기(실버5)
병합 정렬 알고리즘과 동일
// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n, m] = input[0].split(' ').map(Number);
const arrayN = input[1].split(' ').map(Number);
const arrayM = input[2].split(' ').map(Number);
const result = [];
let i = 0;
let j = 0;
while(i < n && j < m) {
if(arrayN[i] < arrayM[j]) {
result.push(arrayN[i]);
i += 1;
} else {
result.push(arrayM[j]);
j += 1;
}
}
while(i < n) {
result.push(arrayN[i]);
i += 1;
}
while(j < m) {
result.push(arrayM[j]);
j += 1;
}
console.log(result.join(' '));
문제 2-1) 두수의 합(실버3)
오름차순 정렬 후 start = 0, end = 마지막 초기화 하여 투 포인터 수행
// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const n = Number(input[0]);
const data = input[1].split(' ').map(Number);
data.sort((a, b) => a - b);
const k = Number(input[2]);
let start = 0;
let end = data.length - 1;
let result = 0;
while(start < end) {
const sum = data[start] + data[end];
if(sum === k) {
result += 1;
start += 1;
} else if(sum < k) {
start += 1;
} else { // sum > k
end -= 1;
}
}
console.log(result);
문제 2-2) 수들의 합2(실버4)
내 답안
// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n , m] = input[0].split(' ').map(Number); // n : 숫자의 수, m : 수열의 합
const data = input[1].split(' ').map(Number);
let start = 0;
let end = 0;
let result = 0;
let sum = 0;
while(start < n) {
while(end < n && sum < m) {
sum += data[end];
end += 1;
}
if(sum === m) result += 1;
sum -= data[start];
start += 1;
}
console.log(result);
강의 답안
// 입력 생략
let cnt = 0;
let intervalSum = 0;
let end = 0;
// start를 차례대로 증가시키며 반복
for(let start = 0; start < n; start++) {
// end를 가능한 만큼 이동 시키기
while(intervalSum < m && end < n) {
intervalSum += data[end];
end += 1;
}
if(intervalSum === m) cnt += 1;
intervalSum -= data[start];
}
console.log(cnt);
문제 2-3) 집배원 한상덕(플래티넘5)
- 투 포인터, DFS
Ch 12. 누적합
문제 1-1) 합 구하기(실버3)
// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const n = Number(input[0]); // 데이터 정보
const num = input[1].split(' ').map(Number);
const m = Number(input[2]); // 구간 정보
const line = input.slice(3, m + 3).map(data => data.split(' ').map(Number));
const prefixSum = [0];
let value = 0;
for(let _n of num) {
value += _n;
prefixSum.push(value);
}
let result = "";
for(let [i, j] of line) {
result += `${prefixSum[j] - prefixSum[i - 1]}\n`;
}
console.log(result);
문제 1-2) 나머지 합(골드3)
- 부분합, 조합, 나머지 연산 응용하여 아이디어 도출하는 게 매우 힘들었던 문제 ( 2일 소요 )
- 1차원 배열에서 구간합, 부분합 배열, 부분합 각 인덱스별 나머지 연산 배열, 나머지 연산(0 ~ M-1) 에 대한 카운팅 필요
- modula operator(나머지 연산, mod, %) 의 수학적 기법 요함
핵심 아이디어 (유튜브 참고)
1. (A + B) % C 는 ((A % C) + (B % C)) % C 와 같다.
이는 구간 합의 나머지 연산을 한 값과 특정 구간 수들의 나머지 연산을 더해 나머지 연살을 한 값은 동일하다.
# 입력 예시 1 2 3 1 2 참고
예) (1 + 2 ) % 3 = ((1%3) + (2%3)) % 3
2. 구간 합 배열을 이용한 식 S[i] - S[j] 는 원본 리스트의 j + 1부터 i 까지의 구간 합이다. (또는 S[end] - S[start - 1])
3. S[i] % M = S[j] % M 인 경우 (S[i] - S[j]) % M = 0 이다. 즉, 구간 합 배열의 원소를 M으로 나눈 나머지로 업데이트 하고 S[i], S[j] 가 같은 (i, j) 쌍을 찾으면 원본 리스트에서 j + 1부터 i 까지의 구간 합이 M으로 나누어 떨어진다는 것을 알 수 있다.
- 문제에서 M으로 나누어 떨어지는 구간합(S[i] - S[j])을 구하라고 했으니 (S[i] - S[j]) % M = 0 식이 도출 가능함
- 누적합을 M으로 나눈 나머지 값 중, 동일한 나머지를 각 카운트하여 카운팅한 개수 중 2개를 뽑는 (구간합을 구하기 위한 점화식) 경우의 수를 구하는 조합(Combination, nCr) 문제*
- 예로 나머지가 0이되는 인덱스가 4개(0,2,4,5)일때 그중 2개를 뽑아 구간합을 구하면 조건 만족 한다는 말
2, 3번은 증명하기 전까지 무슨 말인지 이해하기 너무 어려웠다. (또한, 강의 해설에서도 생략하는 말이 너무 많아서 이해가 되지 않았다)

*2번 증명
i = 4, j = 3일때 S[4] - S[3] = 7- 6 = 1 (j + 1부터 i까지 구간합일 때, 4 ~ 4 까지의 구간합 1과 동일)
(강의 버전) start = 4, end = 4일때 S[end] - S[start - 1] = S[4] - S[3] = 7 - 6 = 1

i = 3, j = 1일때 S[3] - S[1] = 6 -1 = 5 (2 ~ 3까지의 구간합 5 와 동일)
(강의 버전) start = 2, end = 3 일때 S[end] - S[start - 1] = S[3] - S[1] = 5

*3번 증명
(S[i] - S[j]) % M = 0 조건 증명
*카운터 {'0' : 4} 의 경우 - arr 배열의 0, 2, 3, 5 인덱스에 대한 2가지 조합을 뽑으면 공식이 증명됨
1) i = 2, j = 0 인 경우
(S[2] - S[0]) % 3 = (3 - 0) % 3 = 0
2) i = 3, j = 0 인 경우
(S[3] - S[0]) % 3 = (6 - 0) % 3 = 0
3) i = 5, j = 0 인 경우
(S[5] - S[0]) % 3 = (9 - 0) % 3 = 0
4) i = 3, j = 2 인 경우
(S[3] - S[2]) % 3 = (6 - 3) % 3 = 0
5) i = 5, j = 3 인 경우
(S[5] - S[3]) % 3 = (9 - 6) % 3 = 0
6) i = 5, j = 2 인 경우
(S[5] - S[2]) % 3 = (9 - 3) % 3 = 0
카운터에서 0번 인덱스( 나머지 0 해당 ) 하는 숫자 4개에 대해 2를 뽑은 조합을 나열하였다.
부분합에서 나머지 0일 수 밖에 없기 때문에 연산 결과도 무조건 M(=3)에 대한 나머지가 0인 것을 확인가능
* 카운터 {'1' : 2} 의 경우 - arr배열의 1, 4 중 2개를 뽑은 조합을 공식 증명
1) i = 4, j = 1 인 경우
(S[4] - S[1]) % 3 = (7-1) % 3 = 0
// S[4] = 1,2,3,1 / S[1] = 1 에 해당
그래서 결과(조합) 7이 구해짐
arr, 누적합 배열에 0번 인덱스를 넣는 것 또한 누적합 연산의 편의성 뿐만아니라, 기법이 었다는 것을 깨달음
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n, m] = input[0].split(' ').map(Number);
const arr = [0, ...input[1].split(' ').map(Number)];
let sum = [0];
for(let i = 1; i <= n; i++) {
sum[i] = sum[i - 1] + arr[i];
}
const processed = []; // 누적합 (prefix sum)을 M으로 나눈 나머지
const counter = {}; // 각 나머지 값에 대한 개수를 저장하고 있는 카운터 (객체)
for(let i = 0; i <= n; i++) {
processed[i] = sum[i] % m;
if(processed[i] in counter) counter[processed[i]] += 1;
else counter[processed[i]] = 1;
}
let result = 0;
for(let i = 0; i < m; i++) { // 0 ~ m-1
// counter[i]개에서 2개를 고르는 조합
if(i in counter) result += parseInt(counter[i] * (counter[i] - 1) / 2);
}
console.log(result);
참고.
알고리즘 코딩테스트 문제풀이 강의 - 5 나머지 합 구하기 (백준 10986)
문제 2-1) 2차원 배열의 합(실버5)
2차원 배열의 누적합 O(N^2)으로 구할 경우
- row 단위로 구한 후 col 단위로 누적합 연산하여 결과를 구한다

O(N^2)으로 풀 경우
// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n , m] = input[0].split(' ').map(Number); // 행, 열
const matrix = [];
let index = 1;
const lines = input.slice(index, n + 1).map(line => matrix.push(line.split(' ').map(Number)));
index += n;
const k = Number(input[index++]);
const request = input.slice(index, index + k).map(data => data.split(' ').map(Number));
for(let [i, j, x, y] of request) {
let sum = 0;
for(let a = i - 1; a <= x - 1; a++) { // i ~ x
for(let b = j - 1; b <= y - 1; b++) { // j ~ y
sum += matrix[a][b];
}
}
console.log(sum);
}
점화식을 사용하여 풀 경우 공간은 더 잡지만, 시간은 좀 더 빨리 연산되는 결과 확인 가능

// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n, m] = input[0].split(' ').map(Number);
const arr = [new Array(m + 1).fill(0)];
for(let i = 1; i <= n; i++) {
arr.push([0, ...input[i].split(' ').map(Number)]);
}
const k = Number(input[n + 1]); // 쿼리의 수(k)
let quries = []; // 각 쿼리 정보 배열
for(let line = n +2; line <= n + 1 + k; line++) {
let [i, j, x, y] = input[line].split(' ').map(Number);
quries.push([i, j, x, y]);
}
// (1,1)부터의 누적합(sum) 계산
const sum = [];
for(let i = 0; i <= n; i++) sum.push(new Array(m + 1).fill(0)); // 0 행 0열을 초기화 해줌으로써 점화식을 사용가능
for(let i = 1; i <= n; i++) {
for(let j = 1; j <= m; j++) {
sum[i][j] = arr[i][j] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1];
}
}
for(let [i, j, x, y] of quries) {
let current = sum[x][y] - sum[i-1][y] - sum[x][j-1] + sum[i-1][j-1];
console.log(current);
}


query1. (1,1) ~ (2,3) // (i, j) ~ (x, y)
구간합 = sum[2][3] - sum[0][3] - sum[2][0] - sum[0][0] = 63 - 0 - 0 - 0 = 63
query2. (1,2) ~ (1,2)
구간합 = sum[1][2] - sum[0][2] - sum[1][1] - sum[0][1] = 3 - 0 - 1 - 0 = 2
query3. (1,3) ~ (2,3)
구간합 = sum[2][3] - sum[0][3] - sum[2][2] - sum[0][2] = 63 - 0 - 27 - 0 = 36
문제 2-2) 부분합(골드4)
- 투 포인터 방식과 누적합(sum)으로 풀이 (시간/공간 복잡도 : O(N))
// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n, s] = input[0].split(' ').map(Number);
const data = input[1].split(' ').map(Number);
const INF = 1e9;
let result = INF;
let sum = 0;
for(let start = 0, end = 0; start < n; start++) {
while(end < n && sum < s) {
sum += data[end];
end += 1;
}
if(sum >= s) {
result = Math.min(result, end - start);
}
sum -= data[start];
}
console.log(result === INF ? 0 : result);
강의 해설
// SUCCESS
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const [n, s] = input[0].split(' ').map(Number);
const arr = input[1].split(' ').map(Number);
let result = 1e9;
let start = 0;
let end = 0;
let summary = arr[0];
while(true) {
while(end < n -1 && summary < s) {
end += 1;
summary += arr[end];
}
if(summary >= s) {
result = Math.min(result, end - start + 1); // 최소 길이 계산
}
summary -= arr[start];
start += 1;
// 탈출 조건 유의
if(start >= n) break;
}
console.log(result === 1e9 ? 0 : result);
문제 2-3) 컬러볼(골드3)
공 크기 순으로 오름차순 정렬 후
- "결과 (공) = 누적합 - 같은 색상 공의 누적합" 으로 결과 값을 구함
- 공 크기에 대한 누적합과 색상별로 누적합을 생각하지 못함
강의 해설에서 누적합(summary) 0, 3, 11, 21 으로 설명하는 부분이 이해 되지 않았는데,
0인 이유는 제일 작은 공(1,3,3)보다 작은 공은 존재하지 않기 때문이고, 그 다음 (4,8,4)의 경우 작은 공인 (1,3,3)이 있기 때문에 "결과(4번 공) = 3 - 0 (앞서 같은 색상 누적합이 없으니) = 3" 이 됨

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const n = Number(input[0]);
const arr = [];
for(let i = 0; i < n; i++) {
// 색상c와 크기 s를 입력받기
let c = Number(input[i+1].split(' ')[0]);
let s = Number(input[i+1].split(' ')[1]);
arr.push([c, s, i]); // 색, 크기, 공 번호
}
// 크기 기준으로 오름차순 정렬
arr.sort((a, b) => a[1] - b[1]);
let summary = 0; //전체 누적합
let colorSummary = Array(200001).fill(0); // 색상별 누적 합
let result = Array(n).fill(0); // 공의 등장 순서(i)별 최종결과
let start = 0;
while(start < n) {
// 크기가 같은 공의 마지막 인덱스 찾기
let end = start;
while(end < n && arr[start][1] == arr[end][1]) end += 1;
// 결과(공 번호) = 자기보다 작은 공들의 크기 합 - 같은 색상인 공들의 크기합
for(let i = start; i < end; i++) {
result[arr[i][2]] = summary - colorSummary[arr[i][0]];
}
// 누적합(합계값) 갱신
for(let i = start; i < end; i++) {
colorSummary[arr[i][0]] += arr[i][1]; // 색상별 누적합
summary += arr[i][1]; // 전체 누적합
}
start = end;
}
console.log(result.join("\n"));후기 (+사진)
4주차에서는 최단 거리, 투 포인터, 누적합에 대한 학습을 수행했다.
최단 거리에서 한 가지 수확이 있다면 다익스트라 알고리즘에 필요한 우선 순위 큐 (PriorityQueue)를 강의에서 추천해준 모듈을 분석해보고 직접 클래스화 하여 사용할 수 있었다는 점에서 의미가 있었다. 그리고 개인적으로 알고 싶었지만 과거에는 이해하지 못했던 플로이드-워셜 알고리즘에 대해 이해 할 수 있는 점 또한 좋았다.
| 다익스트라 | 플로이드-워셜 | 벨만 포드 | |
| 시간 복잡도 | O(ElogV) | O(V^3) | O(EV) |



투 포인터의 경우 이진 탐색과 비슷하여 대부분의 문제는 쉽게 풀 수 있었으나, 집배원 한상덕 문제(DFS, 투포인터)과 같은 구현 문제에서 막히는 것으로 보아 약점을 극복할 필요성이 느껴졌다.
누적합의 경우 나머지 합/2차원 배열의 합/컬러볼 문제를 풀 때 아이디어가 생각나지 않아 힘들었으나, 이 또한 하나를 배워간다 생각하고 될 때까지 붙잡고 하다보니 이해할 수 있어 하나 또 배웠다는 느낌이 든 챕터였다.
2년전에도 다이나믹 프로그래밍, 그리디 알고리즘은 어려워서 포기하고 다른 부분에 좀 더 집중을 했었는데, 느리더라도 천천히 기법을 익히고 문제 풀이를 통해 다양한 사고를 가질 수 있도록 해야 겠다는 생각이 든다.
https://fastcampus.co.kr/dev_online_upjscodingtest
UPSKILL : Javascript 코딩테스트 131개 예제 & CS지식으로 끝내기 | 패스트캠퍼스
25시간 대비 과정 / '코테 레전드' 유튜버 강사님께 핵심만 배우고 빠르게 합격하세요.
fastcampus.co.kr
본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다.